A De Logaritme

De logaritme is een functie en die als het omgekeerde van een exponentiële functie beschouwd kan worden:

\[ y = ^g\!log(x) \\ g^y=x \]

waarbij \(g\) het grondtal is. Indien het niet meegegeven wordt, veronderstelt men dat \(g\) gelijk is aan \(e = 2.718281828..\) en komt de logaritme overeen met de natuurlijk logaritme dat in België en sommige andere delen van de wereld aangeduid wordt met \(ln(x)\).

Een belangrijke reden om een variabele te transformeren met de logaritme is omdat de verdeling ervan een grote scheefheid vertoond waardoor:

de verdeling moeilijker te interpreteren is en
de verdeling te sterk afwijkt van normaliteit, een assumptie waar erg veel statistieken van afhangen

In het R pakket MASS vinden we een heel simpele dataset mammals met gemiddelde lichaamsgewichten en hersenen-massa’s. Deze data laat het probleem alsook het effect van de log-transformatie visueel zien:

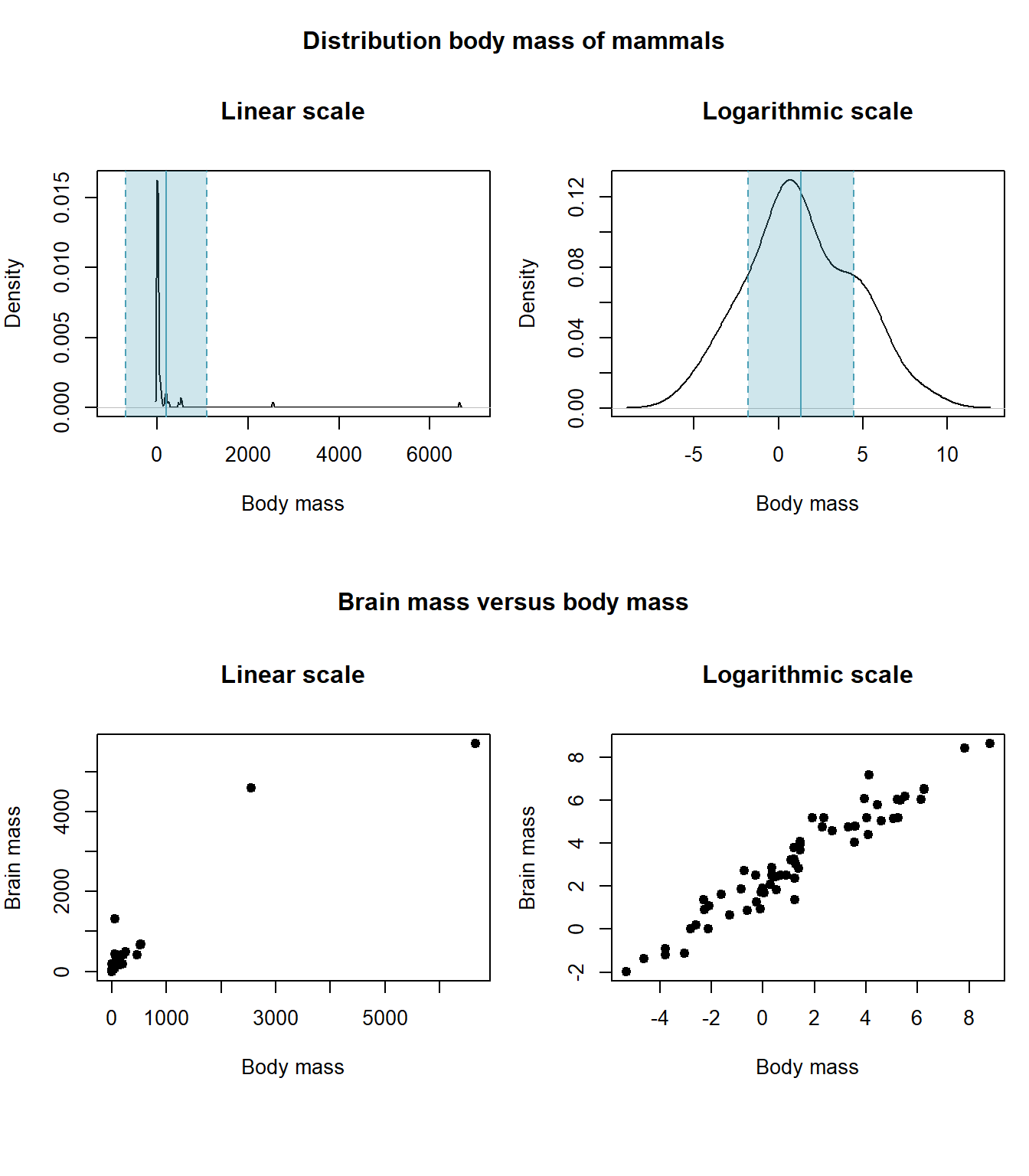
Lichaamsgewichten alleenstaand als verdelingen (boven) of tegenover hersenen-massa’s (onder) in de lineaire schaal (links) of de logaritmische schaal (links). De blauwe balken geven het gemiddelde (volle blauwe lijn) weer ± standaardafwijking (blauwe stippellijnen).

Figuur A.1: Lichaamsgewichten alleenstaand als verdelingen (boven) of tegenover hersenen-massa’s (onder) in de lineaire schaal (links) of de logaritmische schaal (links). De blauwe balken geven het gemiddelde (volle blauwe lijn) weer ± standaardafwijking (blauwe stippellijnen).

Bedenk wel dat enkel strikt positieve lineair-numerieke meetwaarden (\(\mathbb{R}^+\)) voor een log-transformatie in aanmerking komen.

curve(log(x), xlim = c(-5, 10), col = dyad[16], lwd = 2)
polygon(c(-7, -7, 0, 0), c(-3, 3, 3, -3),
  angle = 45, density = 10, col = dyad[16])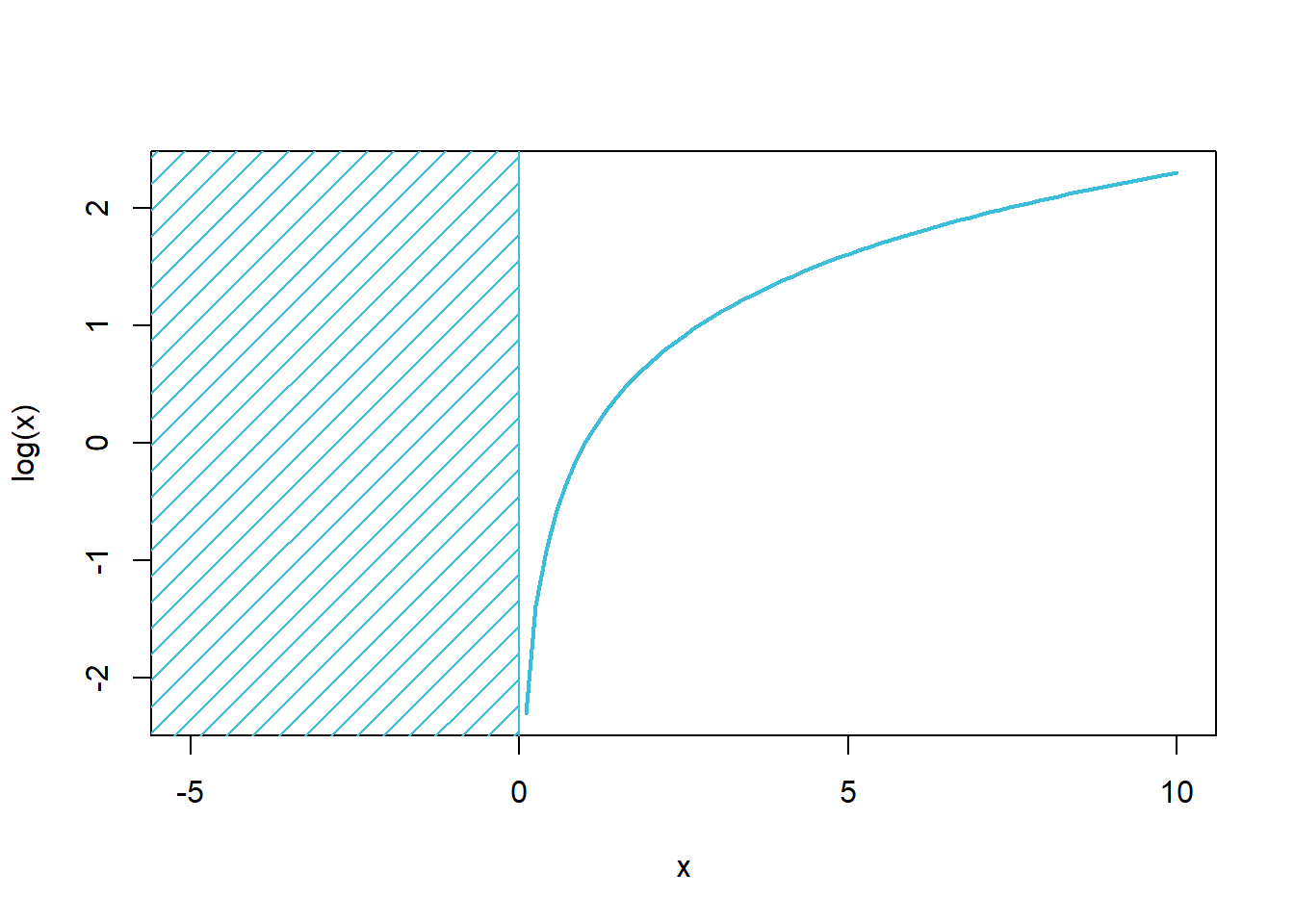

Op internet kan je trucjes vinden om log-transformaties te doen op data die 0 waarden bevatten. Een voorbeeld van zo een trucje is om bij elke waarde ½ bij op te tellen. Zulke procedures kunnen helpen voor de visualisatie maar hebben vaak geen statistische grondslag, dus opgelet hiermee.

We staan er niet meer bij stil hoe fantastisch het eigenlijk is om in een machine log(2.34651) te kunnen opgeven. Wil je weten hoe men vroeger logs berekende? Net als voor andere functies (sin, tanh, …) gebeurde dit aan de hand van tabellen:

Figuur A.2: Zo ging men vroeger te werk voor het berekenen van een logaritme!

Oefening A.1 (Probeer het uit) Maak nu zelf eens een vector van negen waarden gaande van 1E-4 tot 1E4 en neem de logaritme van deze vector.

Oefening A.2 (Anti-log) Deze paragraaf begon met de stelling dat de logaritme als het omgekeerde van een exponentiële functie kan beschouwd worden. Toon dat eens voor jezelf aan. Probeer eens zeer kleine en zeer grote waarden uit voor \(x\) en probeer eens verschillende grondtallen uit.