Hoofdstuk 2 Leren uit data
2.1 Het leerproces
Machine learning (ML) is het vermogen van een algoritme om te leren uit data. In deze inleiding zullen we leren dat, hoewel dit een eenvoudige definitie lijkt, hier toch héél wat achter schuilt. Dus om deze definitie wat kracht bij te zetten, maken we hier meteen ons eerst kadertje voor:
De term word ook ruimer geïnterpreteerd als de discipline die zich bezighoud met het creëren van zulke algoritmen. Laten we eens filosoferen over de term leren in deze stelling. Wat betekent het in feite om iets te leren? Prof. Abu-Mostafa, een gerenommeerde didacticus in deze discipline legt het in zijn boek Learning from data (Abu-Mostafa et al. 2012, p.1) ongeveer zo uit:
Laat een foto aan een driejarige zien en vraag de kleuter of er een boom te zien is en je krijgt bijna zeker het juiste antwoord. Vraag nu aan een dertig-jarige persoon om de definitie van een boom te geven en je krijgt vermoedelijk een onduidelijk of toch onvolledig antwoord.
Hoe komt dit? Een mens leert niet wat een boom is door de wiskundige beschrijving van een boom te memoriseren maar door het beeld te associëren met het woord en de klank en door gecorrigeerd te worden telkens wanneer we een fout maken. De foto’s en tekeningen, de geur, het geritsel van de bladeren, de juf die ‘boom’ zegt, de ouder die wijst, de vier letters op het schoolbord: dat zijn de data. Het verzamelen van al die data en classificeren ervan onder de noemer ‘boom’ gebeurt door onze hersenen en dat proces noemen we leren. Laten we dit schematisch voorstellen:
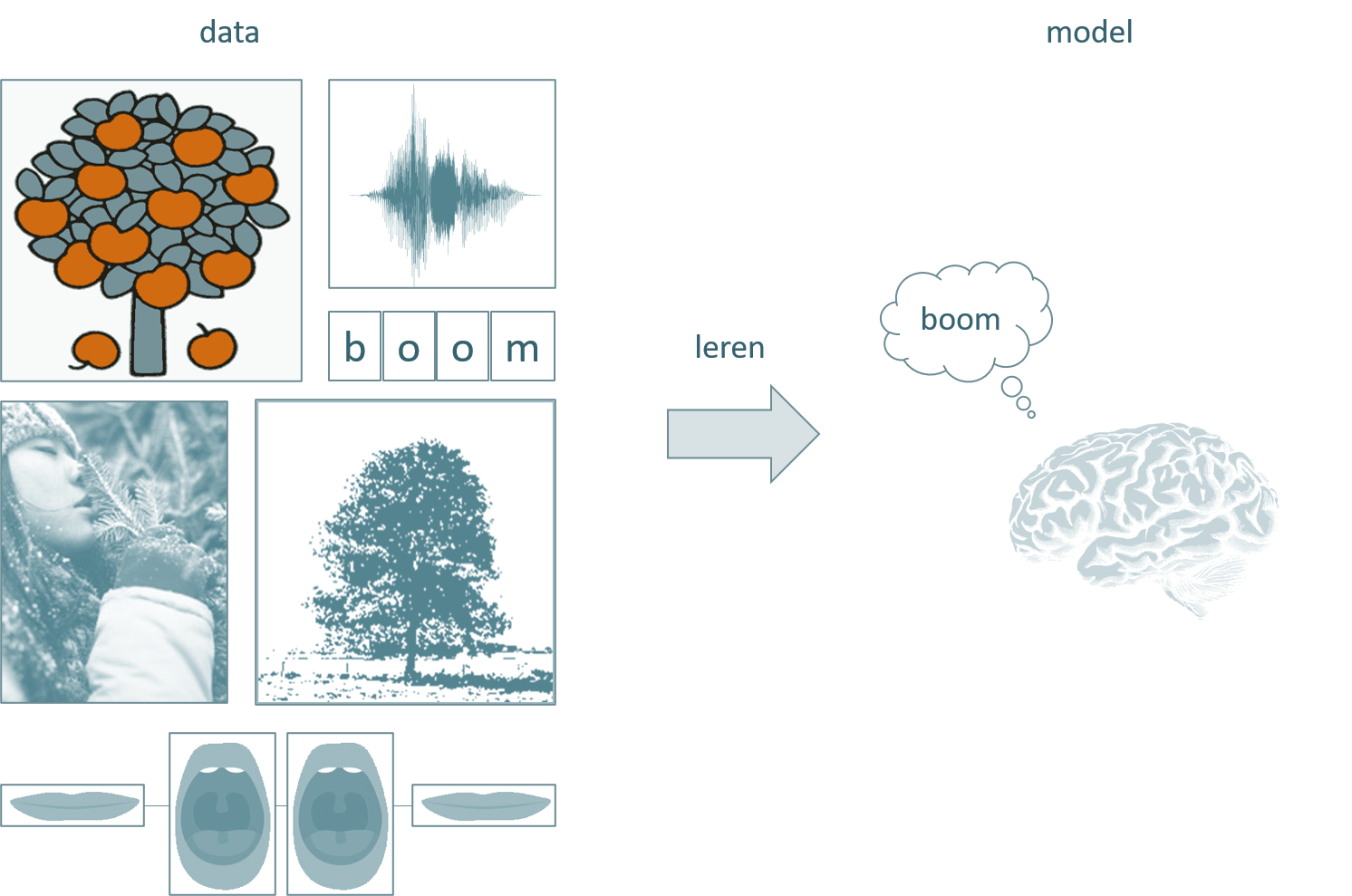
Figuur 2.1: Het centraal zenuwstelsel van een mens kan leren uit data. Het concept ‘boom’ wordt hier met een ‘gedachten-wolk’ voorgesteld en komt overeen met een model van de realiteit.
Het eindpunt van het leerproces is het model. In het voorbeeld van de boom is dit model het concept of mentaal ‘beeld’ van een boom dat in onze hersenen achterblijft ook wanneer we niet naar een boom kijken. Dit model is een vereenvoudigde versie van de werkelijkheid. Het bevat zeker niet alle wiskundige verhoudingen noch alle biologische details van één boom, laat staan van alle bomen op aarde. Toch slagen de meesten onder ons een onderscheid te maken tussen een boom en een niet-boom.
Persoonlijkheid 2.1 (Yaser Abu-Mostafa)

2.2 De evolutie van het machinaal leren
De mens is al eeuwenlang bezig met het bouwen van automaten (zogenaamde automata). Een prachtig voorbeeld hiervan is de geautomatisserde tekenaar-schrijver die de Zwitserse mechanieker Henri Maillardet bouwde rond 1800:
Hierbij ging het meestal om voorgeprogrammeerde robotten zonder enige vorm van intelligentie. Eén van de eerste vormen van meer ‘intelligente’ robotten waren de machina speculatrix van Grey Walters:
Ondertussen weten we dat er zelf-rijdende wagens, zelf-vliegende drones en zelf-varende boten bestaan:
2.3 Intelligentie
ML is een onderdeel van artificiële intelligentie (AI). Er bestaan vele definities voor deze term, maar het VLEVA (Vlaams–Europees Verbindingsagentschap) maakt een duidelijk onderscheid. Zij spreken van ML wanneer patronen in data, al dan niet rechtstreeks afkomstig van sensoren, worden omgezet naar een model, zoals eerder reeds aangehaald. AI gaat een stap verder. Hier wordt er, op basis van het model en nieuwe data, werkelijk ook actie ondernomen en keuzes gemaakt. Bij ML wordt deze fase nog aan de mens overgelaten. Dus zelf-rijdende wagens behoren duidelijk tot het domein van AI, terwijl een applicatie die op basis van een paar fluittonen een melodie kan herkennen eerder thuishoort onder ML. Andere voorbeelden van ML toepassingen zijn het voorspellen van de financiële markten, beeldherkenning, geautomatiseerde medische diagnoses, enz… Dit onderscheid blijft natuurlijk erg artificieel en in sommige gevallen zal deze classificatie niet opgaan. Maar we kunnen wel zeggen:
Maar wat betekent intelligentie in feite? Volgens Wikipedia bestaat intelligentie uit meerdere capaciteiten zoals (logisch) redeneren, begrijpen, zelfbewustzijn, aanleren, emotionele intelligentie, plannen, creatief zijn, kritisch denken en probleemoplossing. Voorlopig ligt de focus bij ML voornamelijk op het aanleren al wordt ook op alle andere aspecten heel wat onderzoek verricht. We moeten voorlopig dus best nog bescheiden blijven met het gebruik van de term artificiële intelligentie. Het is ook heel belangrijk om te realiseren dat er vormen van intelligentie bestaan die erg verschillen van de menselijke intelligentie. Uiteraard wist je dat vele andere dieren aspecten van intelligentie kunnen bezitten. maar wist je ook dat er bij planten vormen van intelligentie werden vastgesteld en dit maakt het des te merkwaardiger gezien zij niet over een centraal zenuwstelsel beschikken.
2.4 Het model
Laten we beginnen met het eindproduct van ML. We zagen dat het eindpunt van ML het model is. In tegenstelling tot wat deze term in bijvoorbeeld database management betekent, kan je het model het best beschouwen als een functie \(\hat{f}\), ook wel de finale hypothese genoemd (final hypothesis; Abu-Mostafa et al. 2012):
\[\hat{f}: \mathcal{X} \to \mathcal{Y}\]
Proberen we nu ons boom-herkenning oefening te vertalen van de menselijke wereld naar de ML wereld, dan bestaat het model uit een functie die een antwoord biedt op de vraag:
Wordt op deze digitale foto een boom afgebeeld?
Nadat de digitale afbeelding een zekere voorbereiding (eng: pre-processing) doorlopen heeft, zal het bestaan uit mogelijk een set van variabelen zoals voorgesteld in figuur 2.2.
Figuur 2.2: Als we de oefening om een boom te herkennen uit figuur 2.1 vertalen naar de machinale wereld krijgen we data van waaruit het algoritme een model heeft aangeleerd. Het model kunnen we hier voorstellen door middel van een functie \(\hat{f}\). Het hoedje op de \(f\) dient om aan te geven dat het om een geschatte waarde gaat.
\(\mathcal{X}\) is hier de input en bestaat in dit voorbeeld uit allerhande variabelen die betrekking hebben op gedigitaliseerde afbeeldingen. Bijvoorbeeld, de variabele Dominante kleur stelt de meest frequente kleur-groep die op de afbeelding voorkomt.
\(\mathcal{Y}\) is de output, de variabele die het antwoord bevat op de vraag of er al dan niet een boom wordt afgebeeld waarbij de witte en zwarte bollen overeenkomen met ja/neen of true/false.
In python zal het model dus ongeveer de volgende vereenvoudigde vorm kunnen aannemen:
en het equivalent in R is als volgt:
2.5 Doelfunctie
Het is je misschien opgevallen dat het symbool voor het model een hoedje draagt: \(\hat{f}\). Dat is geen toeval. Dat wil in feite zeggen dat het om een geschatte functie gaat. Daartegenover staat de werkelijke functie \(f\), de zogenaamde doelfunctie (Abu-Mostafa et al. 2012). Het is belangrijk om te beseffen dat de doelfunctie \(f\) in de meeste gevallen onbekend blijft! Tijdens simulaties of binnen de wetenschappelijke disciplines gebeurt het wel eens dat de \(f\) gekend is, maar in de meeste gevallen waar een datawetenschapper mee te maken krijgt is dat niet het geval. Het doel is uiteraard om te proberen om met het model \(\hat{f}\) de doelfunctie \(f\) zo goed mogelijk te benaderen, en dat valt niet mee als \(f\) onbekend is. Er zijn verscheidene opties om deze benadering tot een succes te maken. Één van deze benaderingen, diegene die we in dit hoofdstuk toepassen, noemt men het begeleid leren (eng: supervised learning).
2.6 MNIST dataset
We gaan nu trachten de eerste ideeën rond ML te vertalen naar de praktijk. Om dit mogelijk te maken, wordt er een nieuwe probleem met bijhorende dataset voorgesteld.
Behalve het begrip ‘boom’ zullen de meeste peuters ook één of ander schrift aangeleerd krijgen. Hoewel gedrukte letters tegenwoordig natuurlijk domineren, wordt er nog steeds het handschrift aangeleerd (figuur 2.3). Behalve mensen is het natuurlijk interessant mocht een computer ook handgeschreven teksten kunnen lezen zodat bijvoorbeeld historische werken gedigitaliseerd kunnen worden.

Figuur 2.3: Het handgeschreven alfabet zoals voorgesteld met de schrijfmethode D’Haese (geen familie; bron).
Om dit mogelijk te maken kan men een model creëren dat in staat is om de handgeschreven karakters te herkennen. Het Amerikaanse Modified National Institute of Standards and Technology biedt een dataset aan met foto’s van handgeschreven letters en cijfers in allerlei varianten. Om de zaak te vereenvoudigen gaan we ons in dit voorbeeld beperken tot de handgeschreven cijfers (figuur 2.4). De cijfers (in de training set) zijn afkomstige van 250 schrijvers, zowel werknemers van de Census Bureau als studenten van het hoger middelbaar onderwijs.

Figuur 2.4: Subset van de MNIST dataset met afbeeldingen van handgeschreven cijfers. Elke geschreven karakter is een afzonderlijke afbeelding van \(28\times28\) pixels. Elke afbeeldingen werd uitgeknipt uit een groter gescand document met geschreven tekst, gecentreerd en teruggebracht naar een grootte van \(28\times28\).
Elke afbeelding in de MNIST dataset wordt voorgesteld als een \(28\times28\)-matrix. Elke element van deze matrix stelt een grijswaarde voor van een pixel uit de afbeelding. Stel dat de afbeeldingen in de RGB kleurruimte zouden zijn opgeslagen, dan zou er voor elke pixel niet één maar drie waarden beschikbaar worden gemaakt.
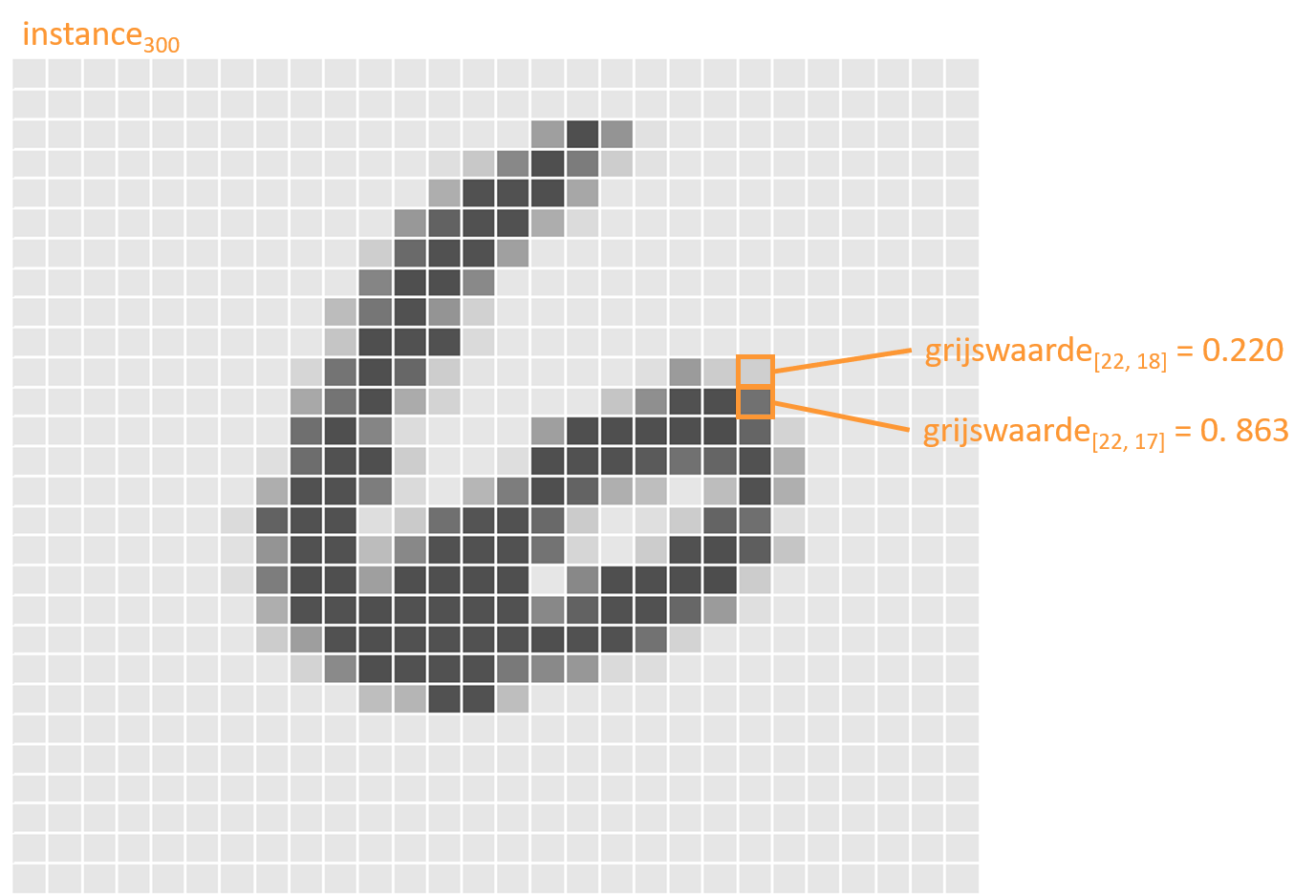
Figuur 2.5: Het 300ste cijfer het de MNIST training-set.
Elke instantie van de input dataset (eng: instance) wordt dus voorgesteld door een \(1\times784\)-vector en de ganse input dataset kan worden voorgesteld als een \(n\times784\)-matrix, waarbij \(n=60\,000\) de grootte van de (training-) dataset is zoals beschikbaar gemaakt door MNIST.
2.7 Het resultaat van MNIST analyse
We gaan later in detail onderzoeken hoe we precies de beeldherkenning kunnen uitvoeren. Nu nemen we eerst een kortere weg naar het resultaat. Kijk even terug naar figuur 2.2 en herinner je dat het resultaat van een ML process een model was dat wiskundig als functie \(\hat{f}\) kan worden voorgesteld. Schematisch zal onze analyse er nu uitzien zoals voorgesteld in figuur 2.6. Merk hier wel op dat de cijfer-varianten in werkelijkheid vervat zitten in een ‘platte’ matrix is met dimensies \(60\,000\times784\), een matrix dus met méér dan 47 miljoen zwevende kommagetallen (eng: floating point).
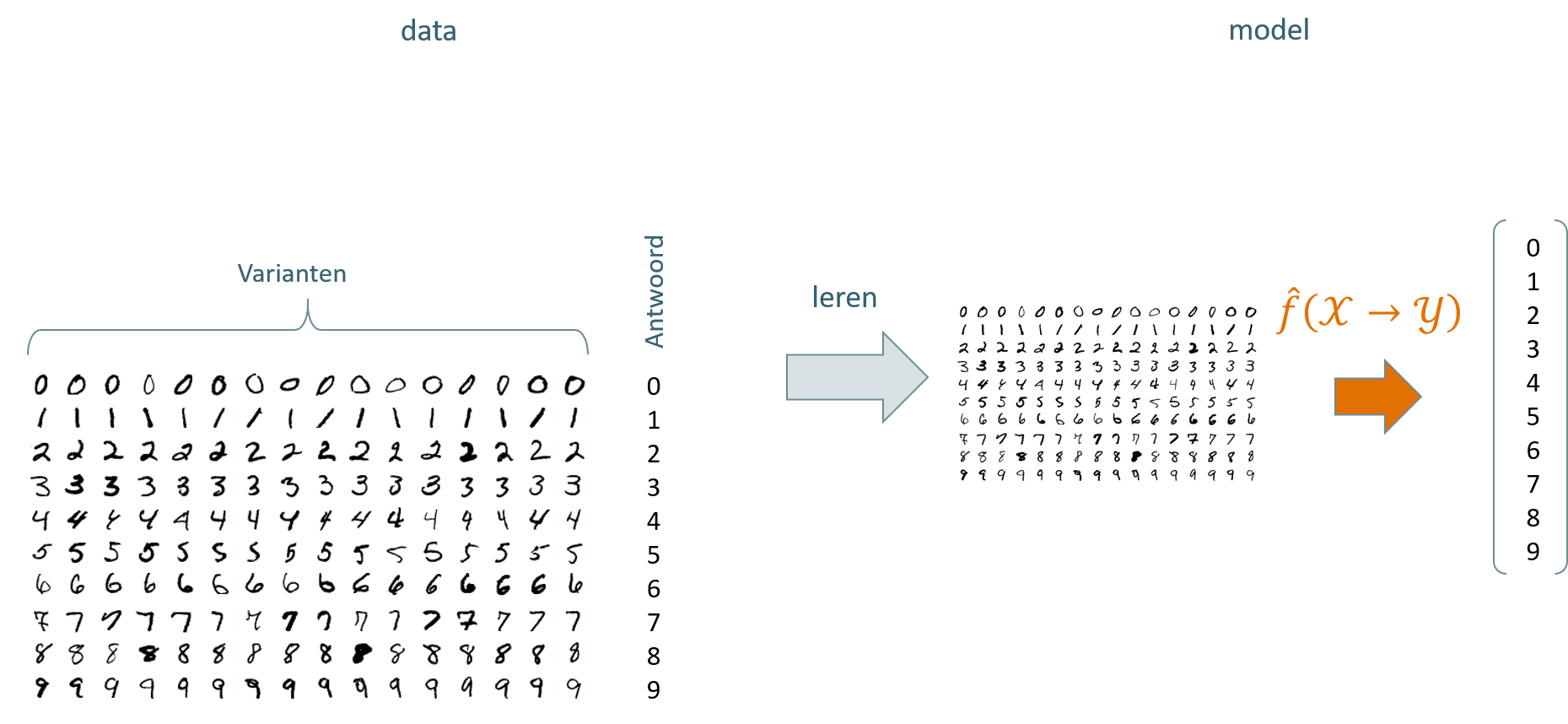
Figuur 2.6: De schematische weergave van het leerproces voor het herkennen van handgeschreven cijfers uit de MNIST dataset.
Stellen we het model voor met de Python functie model, kan kunnen we dit aanroepen met één of meerdere afbeeldingen van handgeschreven cijfers:
Hier roepen we het model aan met de 300ste afbeelding uit de training-set (zie figuur 2.5), hier voorgesteld als x_trn[299:300]. Het resultaat van deze oproep wordt in variabele y_prd_300 bewaard. In wiskundige termen schrijven we \(\hat{y}_{300}\), waarbij het hoedje aangeeft dat het niet de werkelijk \(y\)-waarde is maar de geschatte of voorspelde \(y\)-waarde. In theorie zou men verwachten dat de inhoud y_prd_300 gelijk is aan 6. Het is zeker mogelijk om model zo te schrijven dat dit inderdaad het geval is, maar meestal wordt er de voorkeur aan gegeven om naast de eigenlijke voorspelling ook een maat van de betrouwbaarheid van deze schatting mee te laten geven. In dit geval ziet y_prd_300 er zo uit:
[[1.3147994e-08 4.3827520e-12 5.0856454e-07 1.3127689e-09 4.5237027e-07
5.3989115e-09 9.9999893e-01 5.3377733e-09 1.6693608e-07 3.1370115e-09]]Dit is iets heel anders dan 6, wat is hier gaande? In feite bestaat het model uit de kans dat de aangeleverde afbeelding overeenkomt met één van de 10 mogelijke uitkomsten, namelijk de cijfers 0 tot en met 9:
| Cijfer | \(p(instantie=cijfer|beeld)\) |
|---|---|
| 0 | 1.3147994e-08 |
| 1 | 4.3827520e-12 |
| 2 | 5.0856454e-07 |
| 3 | 1.3127689e-09 |
| 4 | 4.5237027e-07 |
| 5 | 5.3989115e-09 |
| 6 | 9.9999893e-01 |
| 7 | 5.3377733e-09 |
| 8 | 1.6693608e-07 |
| 9 | 3.1370115e-09 |
We zien nu ogenblikkelijk dat \(p(\hat{y}_{300}=6|x_{300}) = 99.99\%\). Dus in plaats dat het model ons het cijfer 6 teruggeeft, geeft het een schatting van de kansverdeling over alle mogelijke uitkomsten \(P(cijfer|beeld)\). Het is dan aan de datawetenschapper om, in samenspraak met anderen binnen het team, de drempelwaarde (eng: threshold) te bepalen tussen wat voldoende zeker is en wat niet. Stel dat we in dit geval de drempelwaarde \(h_\tau=0.99=99\%\) aannemen, dan vertaalt dit inderdaad naar het (in dit geval correcte) antwoord \(\hat{y}_{300}=\hat{f}(x_{300}, h_\tau=0.99)=6\).
2.8 Het MNIST model
We weten nog steeds niet hoe het model voor het herkennen van de MNIST cijfers eruit ziet, laat staan hoe het tot stand is gekomen. Laten we eerst eens proberen na te gaan hoe het model er van binnen uitziet. In dit geval bestaat het model uit een complex netwerk van gewichten \(\mathbf{\theta}\) die in lagen verdeeld zijn (zie figuur 2.7).
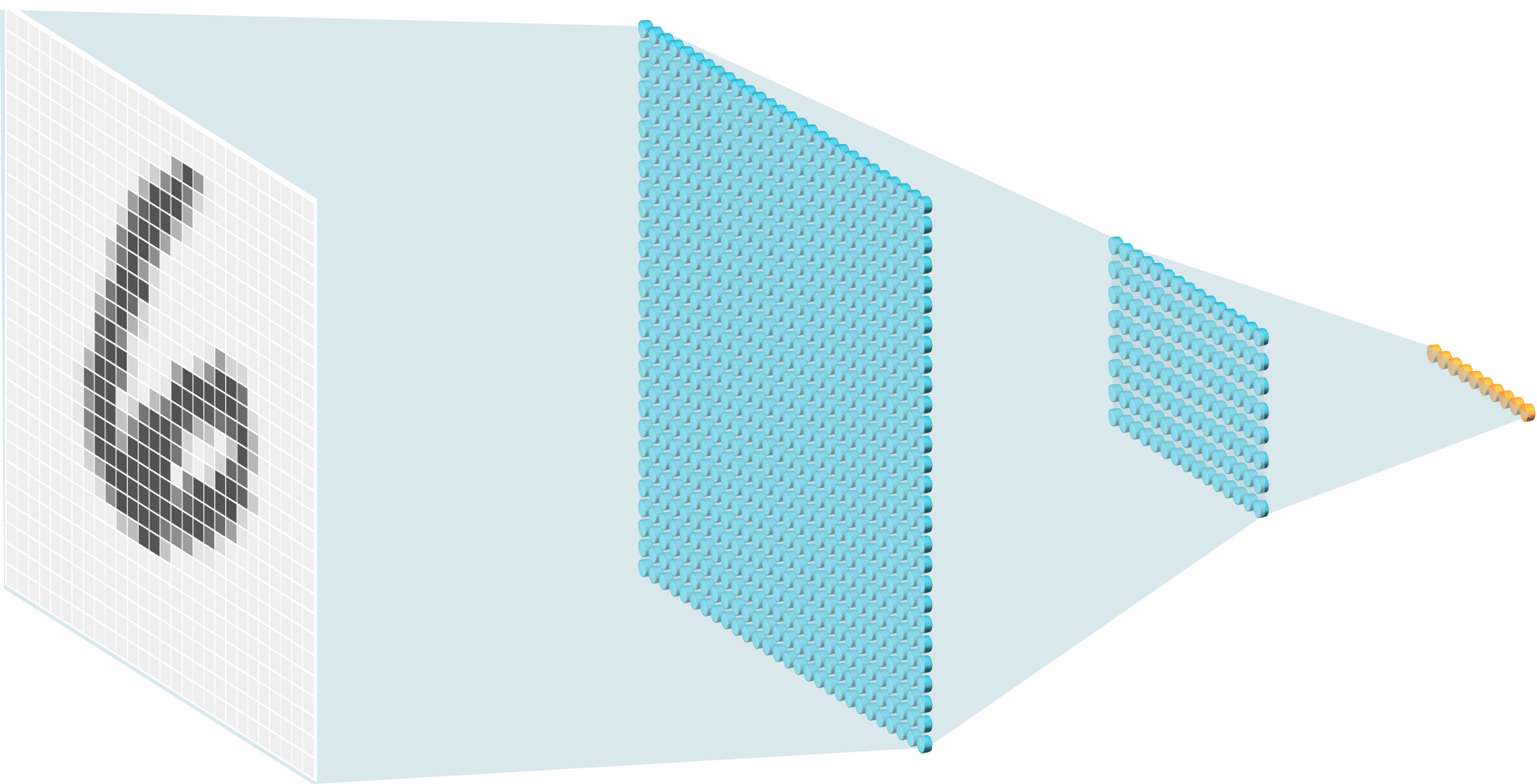
Figuur 2.7: Schematische voorstelling van het MNIST model. Elke grijswaarde (uiterst links) in een afbeelding is verbonden met allerlei noden van de eerste laag in het netwerk (groot blauw raster links) en elke node uit de eerste laag is verbonden met de noden uit de tweede laag (kleiner blauw raster rechts). De oranje balk uiterst rechts stelt het antwoord voor, de kansverdeling over alle mogelijke uitkomsten, zoals uitgelegd in vorige paragraaf.
We kunnen de gewichten uit het model opvragen:
<tf.Variable 'dense_4/kernel:0' shape=(784, 128) dtype=float32, numpy=
array([[ 0.08104221, -0.03245814, 0.05782456, ..., 0.01628028,
0.01527335, -0.0621725 ],
[-0.02486849, -0.05942973, -0.05000503, ..., 0.05511766,
0.01111819, -0.01273195],
...,
[-0.03103521, 0.04082336, -0.03615728, ..., -0.07942228,
0.05170608, -0.04771789],
[-0.08011643, -0.02025594, 0.07396395, ..., -0.04995897,
0.04946151, 0.0736245 ]], dtype=float32)>
[[2]]
<tf.Variable 'dense_4/bias:0' shape=(128,) dtype=float32, numpy=
array([ 0.1288752 , 0.12100432, -0.00982326, 0.1232934 , 0.02084712,
0.01321915, -0.01993161, 0.0420486 , -0.08715703, 0.06092769,
...,
0.11226735, -0.06676487, -0.03609373, -0.05284352, -0.07687864,
0.16832131, 0.08192852, -0.07676063, 0.03645244, -0.04636759,
0.05661207, 0.13083224, 0.02666049], dtype=float32)>In het totaal bestaat deze specifieke versie van het MNIST model dus uit \(784\times128 + 128 = 100\,480\) gewichten. Deze gewichten worden op een nog nader te begrijpen manier gebruikt om \(\hat{y}\) te berekenen uit \(x\). Het model zou er dus ongeveer als volgt kunnen uitzien in Python:
def model(x, tau = 0.99):
weights_0 = array([[ 0.08104221, -0.03245814, ..., 0.04946151, 0.0736245 ]]
weights_1 = array([ 0.1288752, 0.12100432, ..., 0.13083224, 0.02666049]
y_dist = predict(x, weights_0, weights_1)
y_hat_prob = max(y_dist)
y_hat = y_dist.index(y_hat_prob)
if(y_hat_prob < tau):
y_hat = None
return y_hatIn ons voorbeeld zou, indien x overeenkomt met \(x_{300}\) uit 2.5, y_dist overeenkomen met \(P(\hat{y}_{300}|x_{300})\), y_hat_prob met \(99.999893\%\) en y_hat met \(6\). Indien de berekende distributie 10 waarden zou bevatten die allen kleiner zijn dan \(h_\tau\) (tau in de code hierboven), zou dit model aangeven dat er te weinig zekerheid is over welk cijfer de afbeelding moet voorstellen door de waarde None terug te geven.
2.9 Het leerproces voor begeleid ML
Zoals gezegd gaan we nog niet volledig in detail onderzoeken hoe een ML model tot stand komt, maar laten we toch al trachten het ML proces te schematisch reconstrueren, specifiek voor wanneer het gaat om begeleid leren. Wat weten we tot nu toe? We weten dat we vertrekken met training data \(\left(\mathcal{X}_{trn},\mathcal{Y}_{trn}\right)\) en eindigen met een model \(\hat{f}\). We weten ook al dat het model een functie is die test data \(\mathcal{X}_{tst}\) als invoer heeft en een voorspelling (eng: prediction) \(\hat{y}\) als uitvoer (zie Figuur 2.8).
Figuur 2.8: Eerste overzicht van het leerproces voor begeleid ML. Ronde vormen staan voor acties of functies, rechthoekige vormen geven objecten weer. Met andere woorden, het proces voor ML kan gecodeerd worden als \(\hat{f}=\ell(\mathcal{X}, \mathcal{Y})\). \(trn\) staat voor training, \(tst\) voor test. leren: eng. learning, training. voorspellen: eng. to predict, inference.
2.10 De onderdelen van een model
Het model is dus een functie met daarin de gewichten \(\mathbf{\theta}\) alsook de nodige logica om de invoer op de juiste manier te bewerken met de gewichten. Dit laatste wordt in tekstboeken vaak over het hoofd gezien omdat het in de praktijk vaak neerkomt op een eenvoudige matrix vermenigvuldiging. Hier wordt ervoor gekozen om dit een beetje explicieter te maken. In het MNIST model uit vorige paragraaf zien we nog een derde element, het argument \(h_\tau\) (tau in code). Dit is een hyperparameter. Hyperparameters die gekoppeld zijn aan een model dienen vaak, net als bij \(h_\tau\), om een grenswaarde te bepalen tussen wat een goede voorspelling is en wat niet. We zullen in volgende paragraaf zien dat er ook hyperparameters gekoppeld kunnen worden aan het leeralgoritme, waar ze gewoonlijk een heel andere rol gaan spelen.
Stelling 2.6 Het model dat het resultaat is van begeleid machinaal leren bestaat uit minstens 2 onderdelen:
- de gewichten \(\mathbf{\theta}\)
- de modellogica
maar is vaak pas bruikbaar mits het definiëren van nog een derde onderdeel:
- de hyperparameters \(\mathbf{h}_f\)
2.11 Hyperparameters
Hyperparameters worden zo genoemd om ze duidelijk te onderscheiden van gewichten, die in de literatuur ook vaak parameters worden genoemd. Het onderscheid is belangrijk omdat hyperparameters het proces zelf beïnvloeden (e.g. waar moet je de lijn trekken, hoeveel getallen na de komma moet genereren, …) terwijl conventionele parameters het onderwerp zijn van de wiskundige bewerking waarmee invoer wordt omgezet naar een voorspelling.
De manier waarop parameters tot stand komen worden bepaald door het leeralgoritme (zie volgende §). Hyperparameters, daarentegen worden door de datawetenschapper gekozen ofwel in een afzonderlijk proces automatisch geoptimaliseerd. De keuze voor de waarde van een hyperparameter zoals \(h_\tau\) kan gemaakt worden door de datawetenschapper op basis van ervaring ofwel omdat het door de omgeving wordt opgelegd. Laten we twee voorbeelden bekijken die aangeven hoe de omgeving een drempelwaarde kan opleggen.
Voorbeeld 2.1 Stel, er wordt de datawetenschapper gevraagd om een algoritme te ontwikkelen om afbeeldingen van katten en honden (en telkens exact één kat of één hond) te onderscheiden, gewoon voor het plezier. Stel dat het algoritme slechts één waarde uitvoert, namelijk de probabiliteit \(p_{kat}\) dat de afbeelding een kat laat zien. De probabiliteit dat het een hond is (\(p_{niet kat}\)), kan hieruit berekend worden met de formule \(p_{niet kat}=1-p_{kat}\). Een logische drempelwaarde op deze probabiliteiten is \(0.5\). Vanaf dat \(p_{kat}\) zakt onder deze waarde, gaan we ervan uit dat het om een hond gaat.
Voorbeeld 2.2 De datawetenschapper wordt nu gevraagd om een algoritme te ontwikkelen om op basis van tal van bloedwaarden van een patiënt te bepalen of deze ziek is of niet. Het algoritme voert weer slechts één waarde uit, ditmaal de kans om ziek te zijn \(p_{ziek}\). De drempelwaarde mag nu niet meer zo maar op \(0.5\) worden geplaatst. Waarom niet? ML algoritmen maken fouten maar niet alle fouten zijn even erg. Het foutief aanduiden van een gezonde persoon als ‘ziek’ is niet zo erg als het foutief aanduiden van een zieke patiënt als gezond. Maar hoe weet de datawetenschapper dan welke drempelwaarde er gekozen moet worden? Nu komt het: in dit geval mag de datawetenschapper in geen geval een drempelwaarde zelf bepalen. De arsten die de opdracht geven dragen de verantwoordelijkheid om de ideale drempelwaarde te bepalen
2.12 Het leeralgoritme
Om van de training data naar het model te gaan heb je een leeralgoritme \(\ell\) nodig. Voorbeelden hiervan zijn support vector machines (SVM), neuraal netwerken (NN), naïef Bayes algoritmen (NB), enzovoort… Er zijn wel honderden algoritmen waaruit een datawetenschapper kan kiezen, en voor elk algoritme zijn er gewoonlijk oneindig veel mogelijke instellingen1 (lett.). We begrijpen uit vorige paragraaf dat parameters en hyperparameters verschillend zijn maar puur wiskundig beschouwd, dienen ze allebei gewoon als invoer voor de ene of ander functie. Noteren we de hyperparameters bij het leeralgoritme nu als \(\mathbf{h}_\ell\), dan krijgen we het volgende:
\[\hat{f}=\ell\left(\{\mathcal{X}, \mathcal{Y}\}, \mathbf{h}_\ell\right)\]
Hier staat: het ML model wordt, in het geval van begeleid ML, gevormd door een leeralgoritme dat zowel data als invoer heeft (\(\{\mathcal{X}, \mathcal{Y}\}\)) als hyperparameters die het leerproces kunnen beïnvloeden. Wat is dan de rol van de hyperparameters die op het leeralgoritme inwerken? Zonder nu al te veel in gaan op het intern mechanisme van de leeralgoritmen, is één van de veel voorkomende functies van \(\mathbf{h}_\ell\) om te bepalen hoe snel het leeralgoritme te werk moet gaan.
Ik wil hier nog even benadrukken dat het resultaat van het leeralgoritme moet bestaan uit een set van parameters én een functie-logica. Deze functie-logica ligt voor een bepaald leeralgoritme vast. Bijvoorbeeld, voor een logistische regressie, bestaat deze logica uit een logit-transformatie en een matrix vermenigvuldiging. Deze logica plus de parameters \(\mathbf{\theta}\) vormen samen het model. De hyperparameters die op het model inwerken worden, zoals uitgelegd in vorige §, meestal achteraf bepaald door de datawetenschapper of opgelegd door de omgeving.
2.13 Model complexiteit
Merk op dat een ML model niet zo complex hoeft te zijn als dit MNIST model. Het kan best dat een model bestaat uit slecht een handvol parameters. Laten we een voorbeeld in beschouwing nemen.
Voorbeeld 2.3 Een zeer bekende oefen-dataset is de iris dataset waarin afmetingen van de kelkbladen en kroonbladen van drie soorten irissen werden opgenomen.
 Bron: Szczecinkowaty 2007, Mayfield 2005, Mayfield 2007.
Bron: Szczecinkowaty 2007, Mayfield 2005, Mayfield 2007.
Stel dat het doel is om de drie sterk gelijkende bloemensoorten te onderscheiden op basis van slechts 2 variabelen, namelijk de lengte van het kroonblad \(x_p\) en de lengte van het kelkblad \(x_s\). Veronderstel verder dat het model reeds getraind werd. Het model zou bijvoorbeeld kunnen afhangen van slechts 3 parameters die op \(x_s\) en \(x_p\) inwerken, bijvoorbeeld: \(\theta_1 = 2.5\), \(\theta_2 = 1.2\) en \(\theta_3=0.3\). De logica van het model zou er dan bijvoorbeeld als volgt kunnen uitkzien:
\[species=\begin{cases}\text{setosa als }x_p<\theta_1\\\text{versicolor als }x_s>\theta_2p+\theta_3\\\text{virginica anders}\end{cases}\]In dit geval kan de model-logica als volgt gecodeerd worden (Python):
def model(x):
if x.p < 2.5:
return "setosa"
if x.s > 1.2 * x.p + .3:
return "versicolor"
return "virginica"Deze versie van het iris-model met slechts 3 gewichten (parameters!) is wel erg eenvoudig maar er staan ML modellen in productie die niet veel complexer zijn en toch hun werk doen. Complexiteit is trouwens geen goede maatstaf voor de ‘kwaliteit’ van een model. Soms eisen de vragende partij of andere belanghebbenden in het AI project nadrukkelijk een zo eenvoudig mogelijk model zodat het begrijpbaar en transparant blijft. Aan de andere kant bestaan er ook modellen die nog véél complexer zijn dan het MNIST model met honderden miljarden gewichten (\(J > 10^{11}\); Shazeer et al. 2017)!
2.14 Comprimeren door middel van een ML model
Uit de vorige paragraaf leren we dat modellen zeer eenvoudig of zeer complex kunnen zijn. Meestal bevat het model inclusief de gewichten weliswaar véél minder informatie dan de oorspronkelijk data waarop getraind werd. In deze gevallen kan je het model beschouwen als een vereenvoudigde voorstelling van de werkelijkheid of nog als een geavanceerde ‘zip-functie’, hetzij eentje die niet volmaakt is (eng: lossless). Het zou ons te ver leiden om de compressie-factor (eng: compression ratio) te berekenen op basis van de Informatietheorie, maar misschien kunnen we een grove schatting maken van de compressie-factor voor ons MNIST-model (zie Voorbeeld 2.4).
Voorbeeld 2.4 De training set bestaat uit 60 000 afbeeldingen van 28 × 28 pixels. Met de grijswaarden in enkelprecisievariant (eng: single precision) van de zwevendekomma getallen komt de grootte van de training set op:
\[60\,000\times28\times28\times32\approx1.5\cdot10^9 bits\]
Daartegenover bestond het MNIST-model uit \(100\,480\) gewichten:
\[100\,480\times32\approx3.2\cdot10^6 bits\]
Dit brengt ons op een compressie-factor van:
\[\frac{1.5\cdot10^9 bits}{3.2\cdot10^6 bits} > 450\]2.15 Leren versus ontwerp
We hebben al heel wat woorden vuil gemaakt om te begrijpen wat ML eigenlijk inhoud. Laten we nu even stilstaan bij wat ML niet is. Om te beginnen is ML niet ontwerpen. Wat is het verschil? Ook hier is het gemakkelijkste om het verschil aan te tonen aan de hand van twee voorbeelden.
Voorbeeld 2.5 (Ontwerp-benadering verkoopsautomaat probleem) De probleemstelling is als volgt:
Maak een verkoopautomaat die op basis van de massa en de diameter de 4 verschillende Indiase muntstukken (0.5, 1, 2 en 5 Rs) zo goed mogelijk kan onderscheiden.
Oplossing via ontwerp:
Zoek naar de specificaties die gebruikt worden tijdens het ontwerpen van de munstukken. Op de webpagina van Takashi Shimazaki vind je een samenvatting:
| Waarde (Rs) | Massa (\(g\)) | Diameter (\(mm\)) |
|---|---|---|
| 0.5 | 3.79 | 22.0 |
| 1 | 4.85 | 25.0 |
| 2 | 5.62 | 27.0 |
| 5 | 6.00 | 23.0 |
We veronderstellen verder een standaardafwijking op de metingen van \(0.09g\) en \(0.1 mm\) en een fouttolerantie van maximaal 0.1%. Op basis van deze gegevens stellen we een grafiek op en beslissen we ‘met de hand’ waar de grenswaarden worden gedefiniëerd:
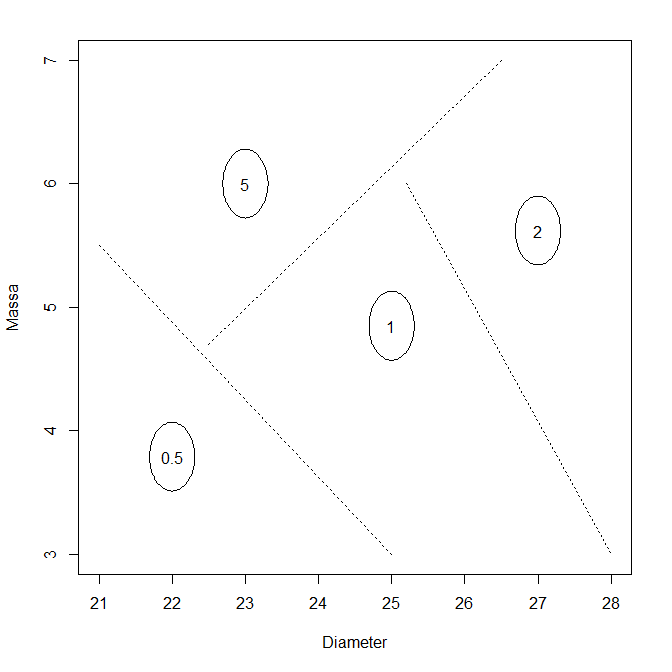
Voorbeeld 2.6 (ML-benadering van het verkoopsautomaat probleem) Oplossing via ML: zoek naar data met werkelijke metingen van de massa’s en diameters van de verscheidene Indiase munstukken. Bij gebrek aan zulke data zit er niets anders op dan een random steekproef te nemen van de munstukken en ze zelf te meten (of door iemand betrouwbaar te laten meten). Hier is het resultaat van de metingen:
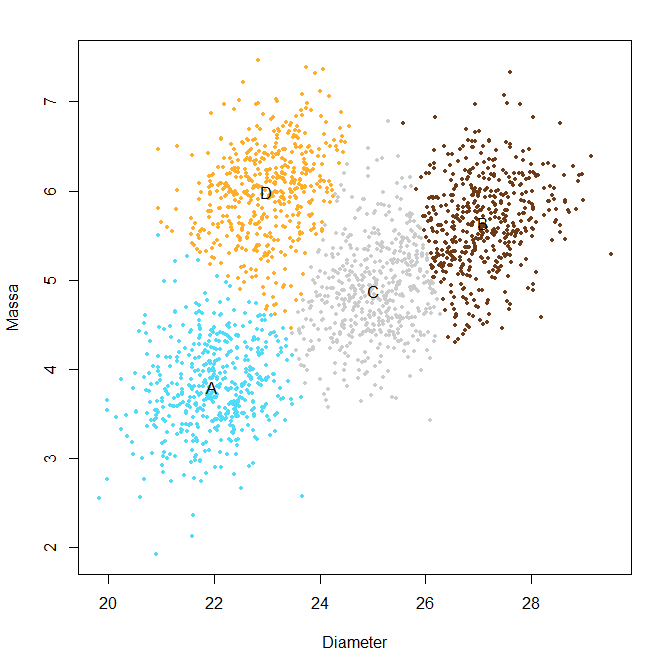
verkoopautomaat-ml
De grafiek voor ontwerp benadering kan je genereren met de onderstaande R code:
library(plotrix)
coins <- fread("
Waarde\tMassa\tDiameter
0.5\t3.79\t22.0
1\t4.85\t25.0
2\t5.62\t27.0
5\t6.00\t23.0")
plot(0, type = "n",
xlim = c(21, 28), ylim = c(3, 7),
xlab = "Diameter", ylab = "Massa")
alpha <- .001
dummy <- coins[, draw.ellipse(Diameter, Massa,
qnorm(1 - alpha, 0, 0.1), qnorm(1 - alpha, 0, 0.09))]
segments(c(25, 22.5, 25.2), c(3, 4.7, 6),
c(21, 26.5, 28), c(5.5, 7, 3), lty = 3)
dummy <- coins[, text(Diameter, Massa, Waarde)]Hieronder vind je de code terug voor de ML-benadering uit Voorbeeld 2.6. Merk op dat ik hier, omdat er niet direct data voorhanden was, de data zelf heb gesimuleerd.
library(MASS)
set.seed(42)
# Generating data
copula <- function(lab, n, rho, mu1, mu2, sd1, sd2){
mu <- c(mu1,mu2)
sigma <- matrix(c(sd1 ^ 2, sd1 * sd2 * rho, sd1 * sd2 * rho, sd2 ^ 2),2)
mvrnorm(n, mu, sigma) %>% as.data.table %>%
set_names(c("Diameter", "Mass")) %>%
cbind(Label = lab)
}
coins_meas <-
coins[1, copula("0.5", 500, .3, Diameter, Massa, .8, .5)] %>%
rbind(coins[2, copula("0.5", 500, .3, Diameter, Massa, .8, .5)]) %>%
rbind(coins[3, copula("0.5", 500, .3, Diameter, Massa, .8, .5)]) %>%
rbind(coins[4, copula("0.5", 500, .3, Diameter, Massa, .8, .5)])
# Analyzing data
model <- kmeans(coins_meas, centers = 4, iter.max = 1000)
plot(coins_meas$Diameter, coins_meas$Mass,
xlab = "Diameter", ylab = "Massa",
pch = 19, col = model$cluster, cex = .6)
text(model$centers[,"Diameter"], model$centers[,"Mass"],
LETTERS[1:4])2.16 Leren versus onthouden en inferentie
De moeilijkste te onderscheiden begrippen in de wereld van ML zijn leren versus inferentie. Dit probleem komt trouwens deels overeen met het onderscheid tussen respectievelijk ML en regressie. Zich de moeite getroosten om een model te ontwikkelen heeft alleen maar nut indien het ook achteraf gebruikt zal worden om voorspellingen mee te doen. Met andere woorden om dingen te ontdekken die men (t.t.z. de computer) nog niet wist. Laten we onderstaand voorbeeld onderzoeken om te begrijpen wat het precies betekent om niets nieuw te leren.
Voorbeeld 2.7 (MT cars relatie) De Motor Trend Car Road Tests dataset bevat 10 standaard eigenschappen voor de motoren van 32 automerken zoals verbruik, cilinderinhoud en dergelijke. Deze data zijn net als iris data een waarde geworden in de wereld van de statistiek. De data werd oorspronkelijk verzameld uit het Motor Trend US magazine van 1974 (zie Henderson and Velleman 1981). Geef ?mtcars in R om meer te weten te komen.
Stel nu dat er een theorie bestaat die de cilinderinhoud \(c\) in verband brengt met de massa \(w\) van de wagen door middel van een variant van de zogenaamde hill-functie:
\[c=\theta_1+\frac{\theta_2-(w-\theta_3)^2}{\theta_4^2+(w-\theta_3)^2}\]
De onderzoeker zal trachten deze vraag te beantwoorden. Hij voert een niet-lineare regressie analyse uit. Hierbij zal een zogenaamd optimalisatie-algoritme de 4 parameters wijzigen totdat de functie die zo ontstaat zo goed mogelijk overeenkomt met de aangeleverde dataset. De onderstaande clip brengt dit proces tot leven:
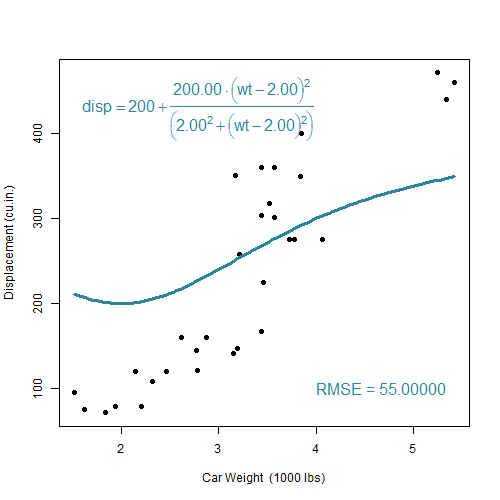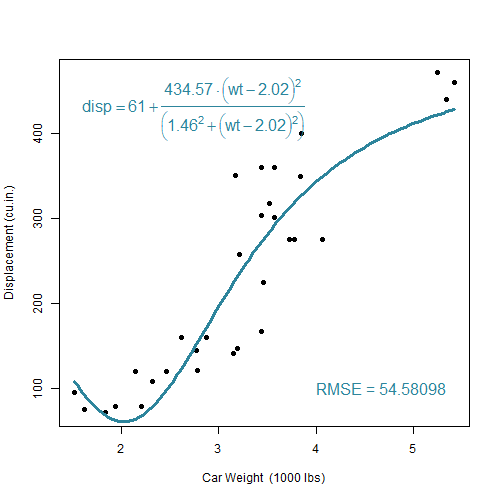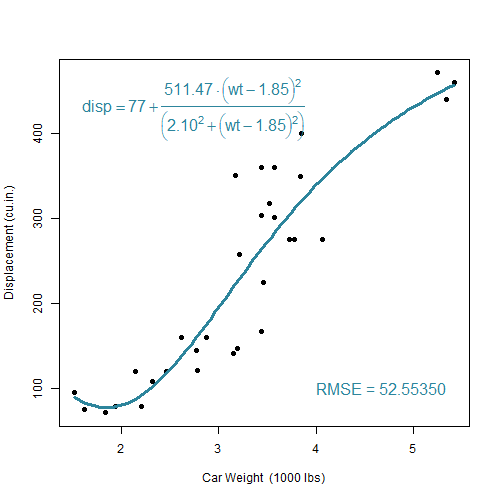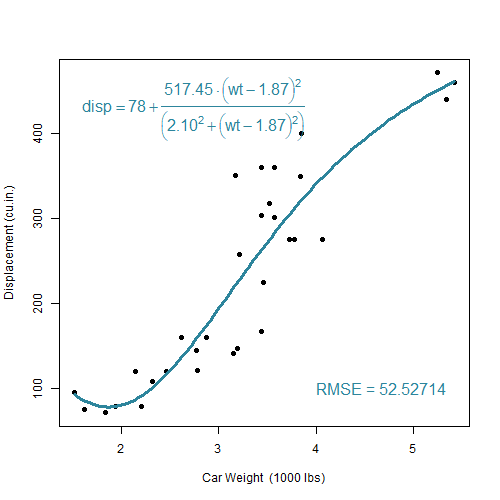
cars-regressie
Naarmate dat de optimalisatie vordert (zie Nelder 1965), verkleint de afwijking tussen voorspelde curve met de datapunten, zoals te zien is aan de zogenaamde Root mean squared Error (RMSE). Op het einde van de optimlisatie, bij een RMSE van 52.527, komt het algoritme tot stilstand met de volgende parameter-waarden:
\[\theta_1=78, \theta_2=517.47, \theta_3=1.87, \theta_4=2.10\]Wat het Voorbeeld 2.7 laat zien is gebaseerd op een vooraf bepaalde model-logica. Van dit model mogen wel de parameters maar niet de complexiteit noch de formule gewijzigd worden. Er kan inderdaad een ideale parameter-set gevonden kan worden die bij deze 32 datapunten past. Maar wat als dezelfde opdrachtgever nu tegen de onderzoeker zegt dat die zich vergist had. Het zou beter zijn om te de puntenwolk te beschrijven door middel van een polynoom van de vijfde graad. De onderzoeker zet zich eraan en schrijft de volgende R code:
rmse <- function(y, x){
sqrt(mean((y - x) ^ 2))
}
model <- lm(disp ~ poly(wt, 5), data = mtcars)
rmse(model$fitted.values, mtcars$disp)Het resultaat is nu een RMSE van 52.492, beter dan het vorige resultaat, alleen ziet de resulterende curve er nu een beetje vreemder uit:
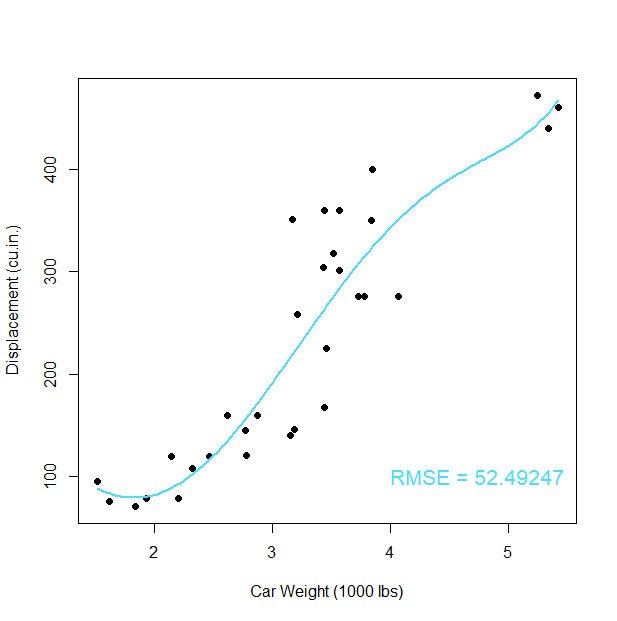
Het probleem is natuurlijk dat hoe hoger de graad van de polynoom, hoe beter de fit zal zijn (is een wiskundige zekerheid) maar ook hoe ‘lelijker’ de curve zal worden:
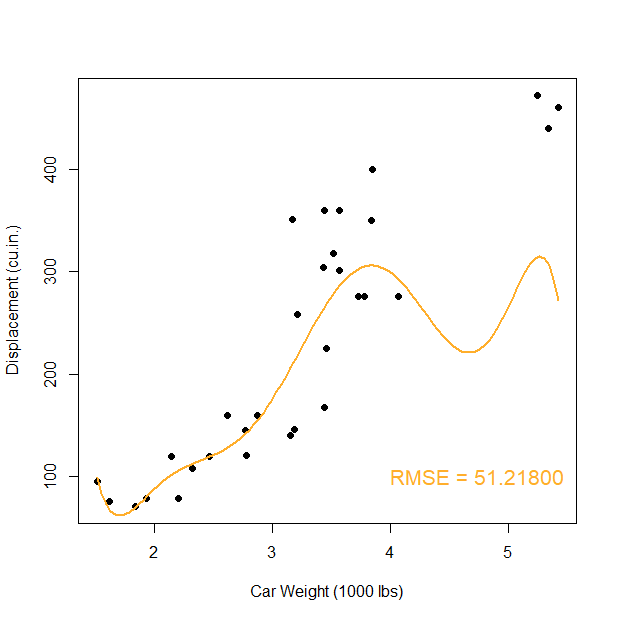
Wat hier aan het gebeuren is noemt met overfit. Een polynoom met zulke hoge graad is veel te complex voor het onderliggend patroon. We voelen dit ergens wel aan. Voordat ML populair was, zou een onderzoeker ‘op het gevoel’ afgaan om de graad van de polynoom te bepalen. In ML wordt de complexiteit niet op voorhand opgegeven en zoekt het leeralgoritme zelf uit hoe complex het model mag worden alvorens er overfit optreedt.
Kunnen we dat overfitten ook formaliseren of zelfs bewijzen? Het antwoord is ja en ja. Het eerste (het formaliseren) zou ons te ver leiden, maar voor de geïnteresseerden raad ik aan om de term VC dimension op te zoeken, genoemd naar twee grondleggers van de ML theorie: Vladimir Vapnik en Alexey Chervonenkis en het boek (of online lezingen) van Yaser Abu-Mostafa (zie (thm: abumostafa)) te bekijken (Abu-Mostafa et al. 2012). Het tweede aspect (het bewijzen) is eenvoudiger. We moeten gewoon op zoek gaan naar nieuwe data:
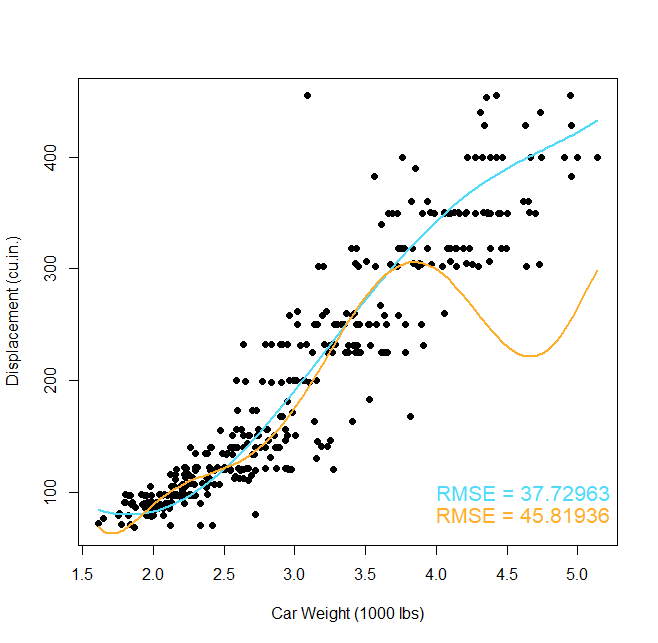
We zien nu het gevolg van overfitting. Wanneer we het model blootstellen aan nieuwe data zien we dat het eenvoudige model (polynoom van graad 5) veel beter presteert dan het complexere model (polynoom van graad 7). En dat is het hem nu net allemaal om te doen! Leren om voorspellingen te maken, niet leren om de training dataset nauwkeurig te beschrijven, want dat is gewoon onthouden of hoogstens comprimeren zoals we eerder zagen. Daarom is ML veel interessanter dan regressieanalyse. Je kan stellen dat regressie (zoals de naam het eigenlijk al aangeeft) gaat over ‘achterom kijken’, terwijl ML gaat over ‘naar de toekomst’ kijken.
2.17 Onbegeleid ML
Tot hier toe werd er voornamelijk gesproken rond begeleid ML (eng: supervised machine learning). Er zijn nog minstens twee andere vormen die binnen sommige disciplines erg populair zijn. In Voorbeeld 2.6 werd wel gesproken van clusters, en dat is een voorbeeld van onbegeleid ML (eng: unsupervised machine learning of self-organization). Het verschil tussen begeleid en onbegeleid is het gebruik van de uitkomsten (\(y\)) als invoer voor het leeralgoritme.
Stelling 2.10 Bij begeleid ML wordt het leeralgoritme getraind op invoer data (\(\mathbf{x}\); de onafhankelijke variabelen) die paarsgewijs gekoppeld zijn met uitvoer data (\(\mathbf{y}\); de afhankelijke variabele of uitkomst). Het algoritme leert de verbanden tussen \(\mathbf{x}\) en \(\mathbf{y}\).
Bij onbegeleid ML is er geen sprake van een uitkomst en leert het algoritme gewoon patronen te herkennen in de invoer data.Figuur 2.9: Vergelijking tussen het proces van begeleid L en het proces van onbegeleid ‘leren’.
Welke van beide moet je nu gebruiken? Heel simpel: als je een betrouwbare uitkomst in je bezit hebt, dan kies je best begeleid ML, omdat deze altijd beter zal presteren. Heb je geen uitkomsten of twijfel je aan de authenticiteit of accuraatheid, dan kan je (tijdelijk) overstappen op onbegeleid leren.
Binnen onbegeleid leren, zijn er twee families die veel gebruikt worden. Eentje is de principale componenten analyse (PCA; eng: principal component analysis), de ander is cluster analyse (eng: cluster analysis). In beide gevallen is het resultaat een categorisatie van de instanties (zoals bijvoorbeeld een clustering) of een set van associaties (zoals bijvoorbeeld aanbevelingen, eng: customer recommendations).
Laten we de discussie van onbegeleid ML afsluiten met een voorbeeld:
Voorbeeld 2.8 Stel, een klant wil een geautomatiseerd systeem ontwikkelen om de scherpte meten van microtoommessen. De klant hoopt dit te kunnen doen a.d.h.v. microscopische opnamen van de snede van het mes, waarvan hieronder een voorbeeld:
Elke pixel in bovenstaande afbeelding bevat een R, een G en een B waarde. Het doel is om de afbeelding om te zetten naar een grijswaarde afbeelding, maar dan wel met de optimale gewichten voor de afzonderlijke R, G en B kleur-kanalen zodat er een maximaal contrast ontstaat. We zien immers dat de snede van het mes groen-achtig en niet wit is en we kunnen dus vermoeden dat de drie kleuren een verschillend gewicht gaan krijgen bij het zoeken naar het hoogste mogelijk contrast. Hieronder wordt de code getoond (imports en een aantal helperfuncties weggelaten; zie broncode voor details):
predict_pca <- function(x, n) {
x$x[, 1:n] %*% t(x$rotation[, 1:n]) %>%
scale(scale = FALSE, center = -1 * x$center) %>%
as.data.table
}
contrast <- function(img) {
img %>%
img_to_dt %>%
prcomp( ~ R + G + B, data = .) %>%
predict_pca(1) %>%
dt_to_img(dim(img)) %>%
grayscale %>%
normalize
}
par(mar = rep(0, 4))
img <- "img/Microtome_knife_5.0_5.0_0097.JPG" %>%
load.image %>%
contrast %>%
plot(axes = FALSE)
De code leest als volgt: Laad de afbeelding Microtome_knife_5.0_5.0_0097.JPG en in de contrast functie: zet je het beeld eerst om naar een data.table met de helper-functie img_to_dt (niet getoond). Start daarna de principale componenten analyse op met de ingebakken stats::prcomp functie. Geef hierbij mee dat de drie kleur-kanalen moeten gebruikt wordt om het grootste contrast te vinden. Neem het resultaat van de analyse en neem de eerste component (de combinatie van R, G, en B-waarden die het meeste variantie verklaart) en voer daarmee de omgekeerde bewerking uit met de predict-pca functie. Het resultaat is dat er een iets beter drempel-waarde (eng: threshold) gevonden kan woorden waarme de messnede geïdentificeerd kan worden:
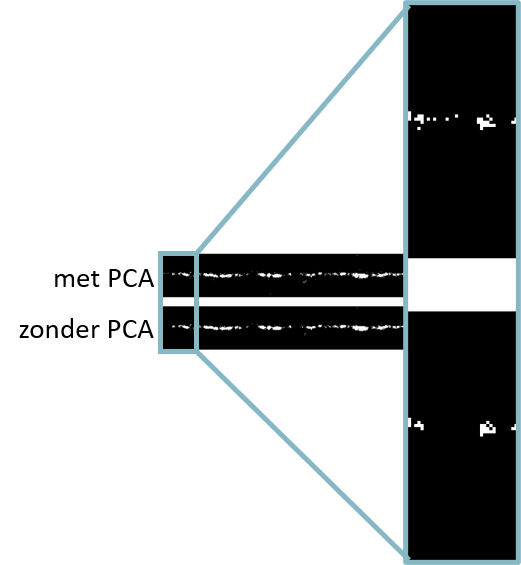
Demo PCA results
Het probleem met onbegeleid ML is dat je nooit zeker weet dat je echt iets geleerd hebt. Bijvoorbeeld, indien een onbegeleid model een nieuwe instantie onderbrengt in een welbepaalde cluster, hoe weet je dan of het juist is of fout? Daarom is die term “onbegeleid leren” mogelijk nogal verwarrend en is het vaak veiliger om gewoon te spreken van clustering (bijv. k-means) of eigen-decompositie (bijv PCA.).
2.18 Conditionering
Er is nog een derde soort ML, namelijk de conditionering (eng: reinforcement learning). In plaats van een afhankelijke variabele, wordt de uitkomst aangeleverd als een functie die, gegeven een bepaalde input zal teruggeven of de nieuwe situatie een verbetering is of niet. Het grootste verschil met de twee eerder besproken vormen van ML is dat er voor conditionering geen nood is aan historische data. In plaats daarvan is er een soort online- data generatie systeem voorhanden. Het is dus in zeker zin supervised, maar toch weer een beetje anders.
Conditionering kent toepassingen in erg veel verschillende disciplines waaronder de statistiek, maar ook de speltheorie, meet- en regeltechniek, operationeel onderzoek, de informatietheorie, enzovoort…. Het werkt zo. Een software-agent (eng: agent) krijgt de keuze uit een aantal acties (eng: actions) die het kan uitvoeren op een omgeving (eng: environment). De omgeving vertaalt de gekozen actie naar enerzijds een toestand-wijziging (eng: state change) en anderzijds een beloning (eng: reward).
Figuur 2.10: Overzicht proces voor conditionering.
We komen later meer uitgebreid terug op conditionering, maar nu houden we het bij een minimalistische implementatie van een soort conditionering, genaamd Q-learning, dit maal in Python. Het voorbeeld is afkomstig van de blog “The Beginner Programmer” van Mic en hetgeen op zijn beurt gebaseerd is op een Q-learning handleiding op de Mnemosyne_Studio blog van John McCullock.
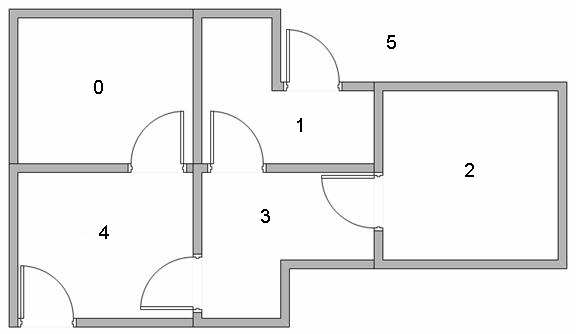
Figuur 2.11: De plattegrond. (bron)
De belonging kan voorgesteld worden als een matrix:
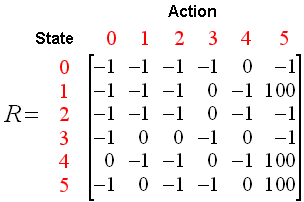
Figuur 2.12: De beloning-matrix ( bron)
import numpy as np
reward = np.matrix(
[[-1,-1,-1,-1, 0, -1],
[ -1,-1,-1, 0,-1,100],
[ -1,-1,-1, 0,-1, -1],
[ -1, 0, 0,-1, 0, -1],
[ -1, 0, 0,-1,-1,100],
[ -1, 0,-1,-1, 0,100]])We maken nu een matrix die het geheugen voorstelt van de tolk. Hierin zal de tolk zijn eerdere ervaringen in opslaan. Dit geheugen stelt de toestand (eng: state) voor waarin de agent zich bevindt. Zoals je ziet weet de agent initieel helemaal niets.
In andere situaties kan het aantal toestanden waarin een agent zich kan bevinden helemaal niet gedefinieerd zijn en dan moet de matrix dynamisch worden opgesteld. Het opvullen van de toestand-matrix gebeurt volgens de onderstaande transitie regel (eng: transition rule):
\[ Q(toestand, actie)=R(toestand, actie)+h_\gamma\cdot max(Q(volgende\,toestand,\,alle\,acties)) \]
We hebben nu een functie die, gegeven een bepaalde toestand, de set van mogelijke volgende toestanden teruggeeft (available_actions) en een tweede die gegeven de mogelijke toestanden er een willekeurige toestand uitkiest (sample_next_action).
def available_actions(state):
current_state_row = reward[state,]
av_act = np.where(current_state_row >= 0)[1]
return av_act
def sample_next_action(available_actions_range):
next_action = int(np.random.choice(available_act,1))
return next_actionTen slotte hebben we een update-functie, de instap-functie a.h.w. van het leeralgoritme, die het geheugen (de toestand-matrix) vernieuwd:
def update(current_state, action, gamma):
max_index = np.where(memory[action,] == np.max(memory[action,]))[1]
if max_index.shape[0] > 1:
max_index = int(np.random.choice(max_index, size = 1))
else:
max_index = int(max_index)
max_value = memory[action, max_index]
memory[current_state, action] = reward[current_state, action] +\
gamma * max_valueWe initialiseren nu het spel met de leersnelheid \(h_\gamma\) en de initiële kamer (2) en de doel-ruimte (buiten, ruimte 5) en voeren de eerste update uit:
Nu begint het trainen (10 000 iteraties):
for i in range(10000):
current_state = np.random.randint(0, int(memory.shape[0]))
available_act = available_actions(current_state)
action = sample_next_action(available_act)
update(current_state, action, gamma)De toestand-matrix er nu zo uit:
model <- as.matrix(100 * py$memory / max(py$memory))
dimnames(model) <- list(start = 0:5, stop = 0:5)
model## stop
## start 0 1 2 3 4 5
## 0 0 0 0.0 0 80 0
## 1 0 0 0.0 64 0 100
## 2 0 0 0.0 64 0 0
## 3 0 80 51.2 0 80 0
## 4 0 80 51.2 0 0 100
## 5 0 80 0.0 0 80 100Nu testen we het model met een begintoestand van 2 en een eindtoestand van 5:
current_state = initial_state
steps = [current_state]
while current_state != end_state:
next_step_index = np.where( \
memory[current_state,] == np.max(memory[current_state,]))[1]
if next_step_index.shape[0] > 1:
next_step_index = int(np.random.choice(next_step_index, size = 1))
else:
next_step_index = int(next_step_index)
steps.append(next_step_index)
current_state = next_step_indexHet aangeleerd pad is als volgt:
## [1] "Ruimte 2 > Ruimte 3 > Ruimte 4 > Ruimte 5"Bronvermelding
Abu-Mostafa, Y.S., Magdon-Ismail, M., Lin, H.-T., 2012. Learning from data. AMLBook New York, NY, USA:
Henderson, H.V., Velleman, P.F., 1981. Building multiple regression models interactively. Biometrics 391–411.
Mayfield, F., 2007. Image of iris virginica shrevei at the james woodworth prairie preserve - a bud and a single flower at full bloom [WWW Document] [Online; accessed 2020-09-07]. URL https://commons.wikimedia.org/wiki/File:Iris_virginica.jpg
Mayfield, F., 2005. Blue flag flower close-up (iris versicolor) at the forillon national park of canada [WWW Document] [Online; accessed 2020-09-07]. URL https://commons.wikimedia.org/wiki/File:Iris_versicolor_3.jpg
Nelder, J., 1965. A. & Mead, r.(1965). The Computer Journal 7, 13.
Shazeer, N., Mirhoseini, A., Maziarz, K., Davis, A., Le, Q., Hinton, G., Dean, J., 2017. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. arXiv preprint arXiv:1701.06538.
Szczecinkowaty, K., 2007. Image of iris setosa in botanical garden in poznań [WWW Document] [Online; accessed 2020-09-07]. URL https://commons.wikimedia.org/wiki/File:Kosaciec_szczecinkowaty_Iris_setosa.jpg
Onder instellingen wordt hier onder andere een combinatie van hyperparameter-waarden verstaan. Omdat deze hyperparameters meestal continue variabelen zijn, maakt dit dat er letterlijk oneindig veel instellingen mogelijk zijn. Bovendien bestaan er voor elke leeralgoritme vaak talrijke varianten, elke met hun eigen voor- en nadelen.↩︎