B Normaliseren versus Standaardiseren

Beide termen worden, vooral in de Engelstalige literatuur, door elkaar gehaald. Hier worden de meer statistische betekenissen van deze termen gehanteerd.

Stelling B.1 (Normaliseren) Een normalisatie van een reeks getallen zorgt ervoor dat de getallen zich tussen een opgegeven minimum en een maximum waarde begeven.

Stelling B.2 (Standaardiseren) Een standaardisatie van een reeks getallen zorgt ervoor dat het gemiddelde van de reeks gelijk wordt aan 0 en de standaardafwijking gelijk wordt aan 1.

Dus, twee transformaties op een reeks getallen die al-bij-al toch vrij verschillend zijn. Hieronder wordt met code en met beelden de verschillen nog verder verduidelijkt. We grijpen hiervoor terug naar de lengtes van de kelkbladen van de irissen.

normalize <- function(x) {
  x_min <- min(x, na.rm = TRUE)
  x_max <- max(x, na.rm = TRUE)
  
  (x - x_min) / (x_max - x_min)
}

x <- iris$Sepal.Length

par(mfrow = c(3, 1), mar = c(4, 5, 5, 2))

x %>% density %>%
  plot(col = 2, main = "Origineel", xlab = "", ylab = "dichtheid")
rug(x, col = 2)

x_norm <- x %>% normalize
x_norm %>% density %>% mirror(0:1) %>% 
  plot(col = 2, main = "Normalisatie", xlab = "", ylab = "dichtheid")
rug(x_norm, col = 2)

x_stand <- x %>% scale
x_stand %>% density %>%
  plot(col = 2, main = "Standaardisatie", xlab = "", ylab = "dichtheid")
rug(x_stand, col = 2)
abline(v = 0, lty = 2)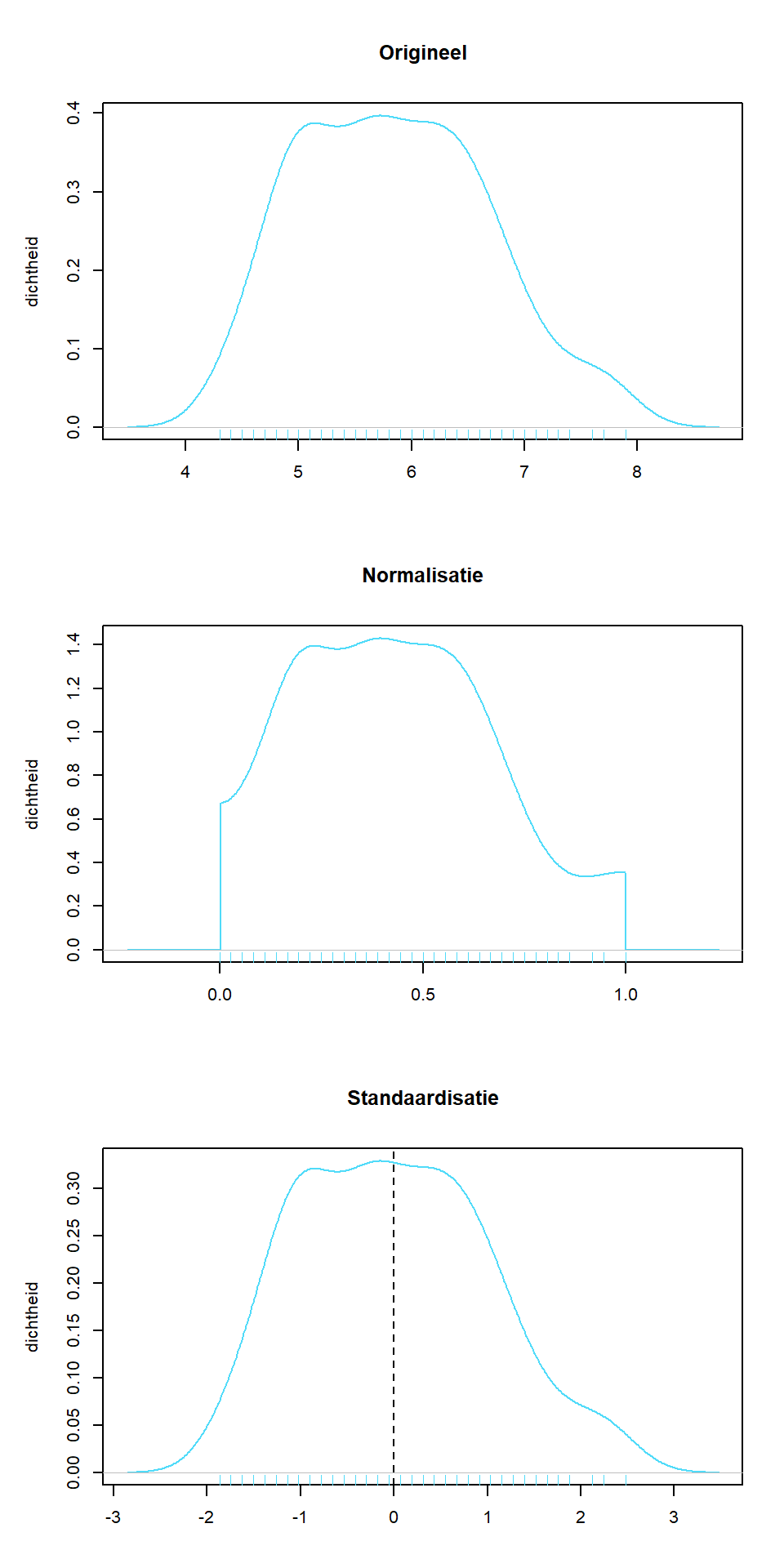

Merk op dat de verdeling grotendeels ongewijzigd blijft, behalve aan de randen bij de normalisatie als gevolg van de mirror-operatie, enkel de x-as wijzigt. De functie mirror is een interne functie op de densiteitscurve (niet de data) binnen de extremen te houden om een wijze die licht verschilt van het cut argument op density.